Difference Between Centre of Gravity and Centroid
The words centre and gravity are derived from the Latin (or Greek) words “centrum” and “gravitatio”. The centre (centroid) represents the centre of mass that is in the cross-section of the diagonals of the body, and gravity – the weight, the attractive force between particles in the universe under which the celestial bodies move.
What is Centre of Gravity?
A centre of mass that, besides centre of gravity, is called a barycentre (the name derives from the Greek word bario, meaning heavy) is the point of an object or system of material points (in ℝ, ℝ2 or ℝ3) in which the whole mass of the object concentrated. This concept allows the whole object to be viewed as one material point whose mass is equal to the total mass of that body. The centre of mass exists for any system of material points, regardless of whether a force is acting on the system or not. The centre of the mass is the point where the gravitational force is acting on the body. The centre of mass can also be located outside the body’s mass limits, which depends on its shape. The centre of gravity of the triangle is in the cross-section of the angle bisections and the centre of gravity of the cube in the cross section of its diagonals. In case of irregular geometric bodies, the centre of gravity is located in the intersection of the gravity lines. This is the point that is at an average distance from all the particles of a system or individual body particle, where the total external force is acting on the particle system or the body. If a particle or body system moves under the influence of an external force, the point at which the centre of gravity is located moves as if it contains all the mass of the system or body. If the body is not with uniform density, the centre of mass (gravity) does not have to be in the geometric centre of the body. The position of the centre of gravity for the particle system in the Cartesian coordinate system is determined by the radius vector rS = Σmiri / Σmi, where mi are the masses of the particles, and ri are the radius vectors of the particles. The position of the centre of the mass of the rigid body in the Cartesian coordinate system is determined by the radius vector rS = (∫rρdV) / M, where r is the unit vector, ρ is the body’s density, V volume, and M is the mass of the body.
What is Centroid?
The geometric centre in referred to as centroid. Simply stated, the centroid corresponds with the centre of gravity in case when the body is homogeneous (with constant density). In physics, centroid of a body is defined as the focus point of the vectors’ collection of the gravitational acceleration of all the material points of the same object. If the body is homogeneous this point is located in the intersection of the gravitational lines, and in right geometric bodies it is determined geometrically. Archimedes was the first to describe the process by which an objects’ centroid can be found. He proposed cutting a cardboard with the objects’ shape and piercing several holes in it. Then nail it on the wall on one of the holes and let it hang freely. Hang plumb on the same nail. Draw with a pencil the direction determined by the direction of the end of the plumb. This direction is called the centre of gravity of the object. Hang the body on the other holes and repeat the procedure.
Difference Between Centre of Gravity and Centroid
1. Definition of Gravity and Centroid
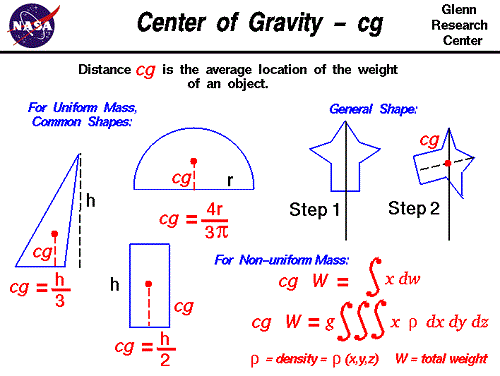
Centre of gravity is the point where the total weight of the body acts while centroid is the geometric centre of the object. Centre of gravity or centre of mass is the point where the whole mass of the body is concentrated. This is where the gravitational force (weight) of the body acts for any orientation of the body. Centroid is the centre of gravity for objects of uniform density.
2. Calculation of Gravity and Centroid
Calculating centre of gravity is not a simple procedure because the mass (and weight) may not be uniformly distributed throughout the object. Centre of gravity can be calculated from cg * W = S x dw where x is the distance from a reference line, dw is an increment of weight, and W is the total weight of the object. Centroid can be found with methods such as the plumb line method discussed above.
Centre of Gravity vs. Centroid: Comparison Chart
Centre of Gravity |
Centroid |
| Centre of mass of a geometric object with any density | Centre of mass of a geometric object of uniform density |
| Point where weight of a body or system may be considered to act | Geometrical centre |
| Denoted by g | Denoted by c |
Summary of Gravity and Centroid
- The gravitational forces of the elementary parts of which the body is composed can be replaced with the action of a resultant force with intensity as large as the weight of the body directed at the centre of gravity of the body.
- The centre of gravity is located in the intersection of the gravitational lines, and in the correct geometric bodies is determined geometrically. This is true if the density of the substance throughout the body is the same, i.e. that the body is homogeneous. In that case the centre of gravity is equivalent with the centroid of the body
- Centroid is the average position of all the points of an object. It is the point at which a cutout of the shape could be perfectly balanced
- Difference Between Thermodynamics and Kinetics - June 24, 2018
- Difference Between Welding and Soldering - June 24, 2018
- Difference Between Additive Colors and Subtractive Colors - June 20, 2018
Search DifferenceBetween.net :
2 Comments
Leave a Response
References :
[0]Dietmar, G., Werner, H., Jörg, S., Wolfgang, A. W. & Nimal, R. “Engineering Mechanics 1: Statics (2nd eds).” Berlin: Springer, 2013. Print
[1]Bapat, R.B. “Linear Algebra and Linear Models (2nd eds).” New York: Springer-Verlag, 2000. Print
[2]Greenberg, M. J. “Euclidean and Non-Euclidean Geometries: Development and History (4th eds).” San Francisco: W. H. Freeman and Co., 2007. Print
[3]"Image Credit: http://waltonaero.wikidot.com/part-d"
[4]"Image Credit: http://thewordplayer.blogspot.in/2008/01/dog-ears-9-blood-meridian-or-evening.html"


Centre of mass doesn’t take account for gravity..
Very nice answer. And explain is good. …..